


The line below shows a part of the Fibonacci series, from 21 to 89, to scale, with 2 Gauges superimposed on adjacent sections of the series to demonstrate that the parts are in the Golden Proportion.
Golden Mean Gauge seen on the right.


No consideration of the Golden Proportion can be complete without mention of the Fibonacci Series which is the complementary view of the Golden Proportion as illustrated above by the 3 Golden Mean Gauges. These numbers are also abundant in the beauty of nature and teeth.
Definition
In this series of numbers each term is the sum of the previous two terms as follows:
|
0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
etc. |
The division of any two adjacent numbers gives the amazing Golden number e.g.
34 / 55 = 0.618 or inversely 55 /34 = 1.618.
It is called the Fibonacci series after Leonardo of Pisa or (Filius Bonacci), alias Leonardo Fibonacci, born in 1175, whose great book The Liber Abaci (1202) , on arithmetic, was a standard work for 200 years and is still considered the best book written on arithmetic. It was the principal means of demonstrating and introducing the enormous advantages of the Hindu Arabic system of numeration over the Roman System.
Leonardo’s reputation amongst scholars was deservedly great. It was so outstanding that King Frederick II, visiting Pisa in 1225, held a public competition in mathematics to test Leonardo’s skill and he was the only one able to answer the questions (Huntley 158).
 One of the most spectacular examples of the Fibonacci Series in nature is in the head of the sunflower.
One of the most spectacular examples of the Fibonacci Series in nature is in the head of the sunflower.
Scientists have measured the number of spirals in the sunflower head. They found, not only one set of short spirals going clockwise from the centre, but also another set of longer spirals going anti clockwise, These two beautiful sinuous spirals of the sun flower head reveal the astonishing double connection with the Fibonacci series.
a. The pairs are always adjacent numbers in the Fibonacci series
e.g. one pair could be 21 and 34 and the next pair could be 34 and 55
b. The adjacent numbers divided yield the Golden Proportion
34 / 55 = 0.618 or 55 / 34 = 1.618
The New Scientist Dec. 81 featured on its cover a daisy head showing the double spiral. The article then went on to discuss the Fibonnaci series, showing other examples of the double spirals in nature and comparing them to computer generated double spirals. The writers also postulated an explanation for the way plants’ growth illustrates the Fibonacci series in the position and spacing of the leaves (Phylotaxis.)

The Muslims allow no illustrations of any of God’s creations and so they were obliged to resort to mathematics to find ways of decorating their places of worship The Fibonacci series features extensively in Islamic decorations. A simplified indication of how a theme could be developed is shown here. The figure above shows 3 diagrams which are the recognisable numbers of the Fibonacci Series in the top line, left side.
The first double digit number is 8 + 5 = 13 but the 13 has been reduced to 3 + 1 = 4 similarly the next double digit 8 + 9 = 17 has been reduced to 8 etc etc . The process called Kabalistic reduction is a frequently used method of manipulating numbers. The next line shows the alternate numbers selected- Excluding 9. From this line a pattern was generated as seen in the 3 figures, related to the number sequence. From this was built the final decorative pattern.
 The adjacent picture shows a design featuring the pentagons and hexagons used in the Mosque. which were developed out of the connections between the Fibonacci series,and the Golden Proportion. The influence and interconnections between Muslim art the Golden Proportion, the polygons, the Vedic Hindu Square and the Cabbala number system, are beautifully illustrated in the “Language of Pattern” by Alburn, Smith, Steel and Walker published by Thames and Hudson.
The adjacent picture shows a design featuring the pentagons and hexagons used in the Mosque. which were developed out of the connections between the Fibonacci series,and the Golden Proportion. The influence and interconnections between Muslim art the Golden Proportion, the polygons, the Vedic Hindu Square and the Cabbala number system, are beautifully illustrated in the “Language of Pattern” by Alburn, Smith, Steel and Walker published by Thames and Hudson.
The Fibonacci Cascade
 The series of numbers below shows a Geometrical progression on the left hand side, where each number, starting from 1, is multiplied by 1.618. On the right hand side the first number is divided by 0.618 giving the identical result for each line. It is most extraordinary to see yet a 3rd simple progression running through the geometric series and that is an arithmetic series arrived at by adding the products of multiplication together as follows:-
The series of numbers below shows a Geometrical progression on the left hand side, where each number, starting from 1, is multiplied by 1.618. On the right hand side the first number is divided by 0.618 giving the identical result for each line. It is most extraordinary to see yet a 3rd simple progression running through the geometric series and that is an arithmetic series arrived at by adding the products of multiplication together as follows:-
Add 1.618 to 2.618 = 4.236 which added to 2.618 = 6.854 etc etc. And this number is the addition of the previous two terms which is non other than the famous Fibonacci Series.
We have thus one progression of numbers, arrived at by three different methods- two geometric and one arithmetic. The two geometric progressions are arrived at by multiplying each term by 1.618 or dividing by 0.168.
|
Multiplication by 1.618 |
Division by 0.618 |
|
1 x 1.618 = 1.618 |
1 / 0.618 = 1.618 |
|
1.618 x 1.618 = 2.618 |
1.618 / 0.618 = 2.618 |
|
2.618 x 1.618 = 4.236 |
2.618 / 0.618 = 4.236 |
|
4.236 x 1.618 = 6.854 |
4.236 / 0.618 = 6.854 |
|
6.854 x 1.618 = 11.09 |
6.854 / 0.618 = 11.09 |
The Mathematical Key
There are different ways to express the simple mathematics of the Fibonacci series.
A mathematician would easily understand that all this stems from the following formula:-
|
1 |
||
|
—– |
= |
1.618 |
|
0.618 |
| The Universe | ||
| ————- | = | The Universe + 0.618 |
|
0.618 |
|
1 |
||||
|
—— |
= | 1.618 | or | Universe + 0 .618 |
|
0.618 |
Where unity implies the ultimate unity
The unity of the Universe divided by ‘something’ is equal to the unity of the universe plus ‘something’.
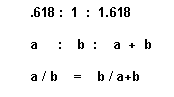
The smaller is to the larger as the larger is to the whole
The Quadratic expression originates here.
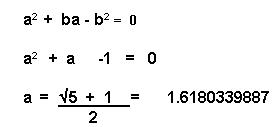

 Phylotaxis is the study of the ordered position of leaves on a stem.( Phyllos-leaf taxis order). (filo pastry– thin leaves of pastry) with particular reference to their repetition in the same alignment
Phylotaxis is the study of the ordered position of leaves on a stem.( Phyllos-leaf taxis order). (filo pastry– thin leaves of pastry) with particular reference to their repetition in the same alignment
The Fibonacci series have been observed in phylotaxis and extensively studied in three different spiral arrangements .
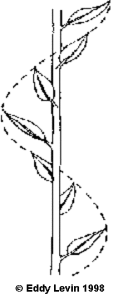
1. VERTICALLY. Where leaves on a stem demonstrate the Fibonacci Series as they spiral up the stem .
2. HORIZONTALLY. Where the spirals are horizontal like on the flat head of the sunflower.
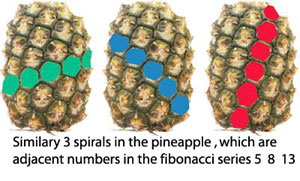
3. TAPERED OR ROUNDED, like the tapered pine cones or the rounded Chrysanthemums or pineapples which also show a double set of spirals as in the adjacent pictures.
 When these double sets of spirals have been counted, the numbers of spirals were found to be the adjacent Fibonacci numbers. Different numbers with different plants. Any textbook discussing mathematics in nature will include numerous examples.
When these double sets of spirals have been counted, the numbers of spirals were found to be the adjacent Fibonacci numbers. Different numbers with different plants. Any textbook discussing mathematics in nature will include numerous examples.
Brian Goodwin in his book, ‘How the Leopard changed its spots’, discusses Phyllotaxis at length and describes a model of phylotaxis produced by two French scientists Douady and Couder. They also managed to reproduce the double spirals of the similar to those of the sunflower by computer.
Brian Goodwin further asks about Phylotaxis. “What is the inherent nature of the simple rules that govern this diversity. What are we looking at when we see such a magnificent variety of plants and flowers?”
The study of Phylotaxis is a branch of biology that seeks the answers to these questions. The connection between phylotaxis and the Golden Proportion has engendered volumes of literature examining these questions. Surprisingly, as recent as 1998, a large magnificent tome on phylotaxis called “Symmetry in Plants” was published as a multidisciplinary study by 44 scientists, all leaders in their fields, including chapters by botanists, mathematicians crystallographers and molecular geneticists.
Phylotaxis-The positions of leaves.
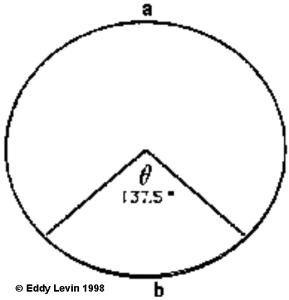 The leaves on a stem are positioned over the gaps between the lower leaves as they spiral up the stem. What is most remarkable about this spiral spacing, is that irrespective of species, the rotation angle tends to have only a few values. By far the most common of which is 137.5 o (Goodwin). This is considered an efficient arrangement to allow maximum sunlight to reach each set of leaves. This angle is non other than the Golden Proportion related to the perimeter of a circle as in the adjacent figure.
The leaves on a stem are positioned over the gaps between the lower leaves as they spiral up the stem. What is most remarkable about this spiral spacing, is that irrespective of species, the rotation angle tends to have only a few values. By far the most common of which is 137.5 o (Goodwin). This is considered an efficient arrangement to allow maximum sunlight to reach each set of leaves. This angle is non other than the Golden Proportion related to the perimeter of a circle as in the adjacent figure.
It is the ratio between the perimeter of a circle where the larger part A, is to the smaller part B, as the larger part A is to the whole A+B. Our old familiar Golden Proportion premise here seen in yet another guise.
The other example of the Golden Proportion is concerned with the number of leaves between one leaf and the next one directly overhead and the number of rotations before this position is reached.
Some trees like Elmwood and basswood, the leaves along a stem seem to occur alternately on two opposite sides and we speak of 1/2 phyllotaxis. In the beech and hazel the passage from one leaf to the next is I/3 of a turn.
oak and apricot 2/5 phylotaxis
poplar and pear 3/8
willow and almond 5/13
these are all recognisable as alternate Fibonacci numbers. {Coxeter}
We have already seen that the number of double spirals of the sunflower head are also Fibonacci numbers. The spirals have perhaps moved from the vertical plane to the horizontal plane.
Sunflower
The Fibonacci numbers also appear when we examine the number of petals of certain common flowers e.g.
| Iris | 3 petals | Daisy | 34 petals |
| Primrose | 5 petals | michaelmas daisy | 55 petals |
| Ragwort | 13 petals | michaelmas daisy | 89 petals |
A brief search at the literature will soon reveal on abundance of further interesting studies on the Fibonacci Series.
Hurrah! In the end I got a web site from where I can truly get useful facts concerning my study and knowledge.
Measurements please of the four arms of the fibonaccl guage.
Hi
Not exactly sure what you are looking for.
The sizes of our standard and basic gauges are approximately 16cm * 6cm when closed and they open to a span of approximately 16cm.
This is a fantastic resource. Please do not let this ever dissapear.